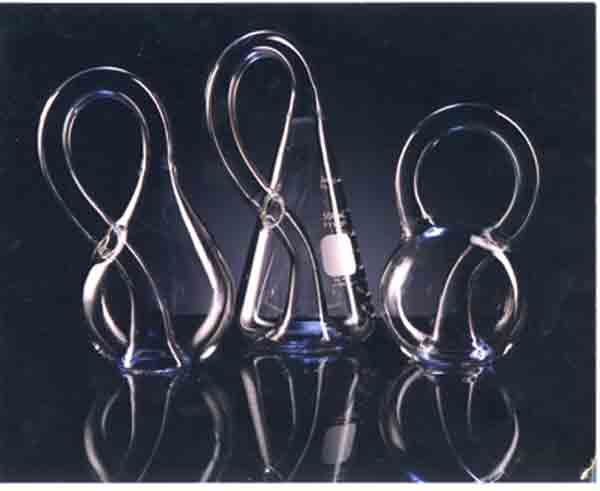
Three glass Klein Bottles, available from Acme Klein Bottle.
|
|
|
Three glass Klein Bottles, available from Acme Klein Bottle. |
Ever hear of a Möbius Loop -- a one sided, one edged surface? Give a strip of paper a half-twist, then tape the ends together. It's one side and one boundary, with delightful properties dear to mathematicians...
|
|
In 1882, Felix Klein imagined sewing two Möbius Loops together to create a single sided bottle with no boundary. Its inside is its outside. It contains itself. Take a rectangle and join one pair of opposite sides -- you'll now have a cylinder. Now join the other pair of sides with a half-twist. That last step isn't possible in our universe, sad to say. A true Klein Bottle requires 4-dimensions because the surface has to pass through itself without a hole. It's closed and non-orientable, so a symbol on its surface can be slid around on it and reappear backwards at the same place.You can't do this trick on a sphere, doughnut, or pet ferret -- they're orientable. |
Alas, our universe has only 3 spatial dimensions, so even Acme's dedicated engineers can't make a true Klein Bottle.
A photograph of a stapler is a 2-dimensional immersion of a 3-dimensional stapler. The true stapler has been flattened into the flatland of the photo. In the same way, our glass Klein Bottles are 3-D immersions of the 4-D Klein Bottle. Acme's Klein Bottle is a 3-dimensional photograph of a "true" Klein Bottle.
A Klein Bottle cannot be embedded in 3 dimensions, but you can immerse it in 3-D. (An immersion may have self-intersections; Embeddings have no self-intersections. Neither an embedding nor an immersion has folds or cusps.)
We represent a Klein Bottle in glass by stretching the neck of a bottle through its side and joining its end to a hole in the base. Except at the side-connection (the nexus), this properly shows the shape of a 4-D Klein Bottle. And except at the nexus, any small patch follows the laws of 2-dimensional Euclidean geometry.
Contrast this with a corked bottle -- say, a wine bottle. It has two sides: inside and outside. You can't get from one to the other without drilling a hole or popping the top. Once uncorked, it has a lip which separates the inside from the outside. If you make the glass arbitrarily thin, that lip won't go away. It'll become more prominent. The lip divides one side of the bottle from the other. So an uncorked bottle is topologically the same as a disc ... it has two sides, separated by a boundary -- an edge.
But a Klein Bottle does not have an edge. It's boundary-free, and an ant can walk along the entire surface without ever crossing an edge. This is true of both theoretical Klein Bottles and our glass ones. And so, a Klein Bottle is one-sided.
A Klein Bottle has one hole. This, in turn, causes it to have one handle. The genus number of an object is the number of holes (well, it's more subtle than that, but I'm not allowed to tell you why). Other genus-1 objects include innertubes, bagels, wedding rings, and teacups. A wine bottle has no holes and so is genus 0. (The genus of a human being is difficult to define because it depends on what you consider a hole -- I'd estimate most people have a genus of 0 to 4, slightly higher when yawning. Pierce your ear and you'll increase your genus by one.)
As an alternative to buying an Acme Klein Bottle, you can save money by just memorizing this set of parametric equations, since it defines the surface of every Klein Bottle.:
x = cos(u)*(cos(u/2)*(sqrt_2+cos(v))+(sin(u/2)*sin(v)*cos(v)))
y = sin(u)*(cos(u/2)*(sqrt_2+cos(v))+(sin(u/2)*sin(v)*cos(v)))
z = -1*sin(u/2)*(sqrt_2+cos(v))+cos(u/2)*sin(v)*cos(v)
or in polynomial form:
![]()
Yep, no doubt about it: Your Acme's Klein Bottle is a real Riemannian manifold, just waiting for you to define a Euclidean metric at every point.
Acme is proud to be our universe's foremost supplier of immersed, boundary-free, nonorientable, one-sided surfaces. We make and sell Klein Bottles.
For more information, on Klein Bottles, visit the Topological Zoo. Or click here to see how to make one in Japan Notice that topologists simulate Klein Bottles ... but ACME makes 'em in glass!
Here's a few other topology links:
Konrad Pollthier of the Zuse Institute / Berlin has written an outstanding article about the Klein Bottle in Plus Magazine (issue 26, Sept 2003). Several sweet applets let you assemble a Klein bottle on your computer screen (but Acme's glass Klein Bottles are made slightly differently!)
Neil Strickland's What is Topology (Did you know that there must be some point on the earth without any wind?)
A friendly, happy view of topology, Klein Bottles, projective planes, spheres, Klein Bottles, curved space, Klein Bottles, manifolds, cosmology, Klein Bottles and more ... read Jeffrey Week's splendid book, The Shape of Space. When Weeks cuts Klein Bottle into two Moebius loops, it looks amazing like how Acme does it.. This book's a perfect introduction to topology - for high school students through postodocs. A perfect match to an Acme Klein Bottle.
Janna Levin's delightful presentation, In space, do all roads lead to home? connects flatland to tiling to space travel ... when studyingcosmology and the shape of the universe, you quickly find yourself thinking about topology!
Here's a mathematical history of topology without any mention of the Klein Bottle!.
You can play TicTacToe on a Klein Bottle.
Nathaniel Hellerstein (a friend of this author) created a Klein Bag from a sock. Works great as a change purse! Endorsed by Cliff Stoll.
Acme Klein Bottles - Exclusive Purveyors of the Non-Orientable
This page last updated December 2021 If any of these links have disappeared, or if you have suggestions, please send me email! Thanks, -Cliff